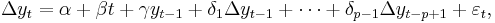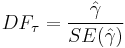Augmented Dickey–Fuller test
In statistics and econometrics, an augmented Dickey–Fuller test (ADF) is a test for a unit root in a time series sample. It is an augmented version of the Dickey–Fuller test for a larger and more complicated set of time series models. The augmented Dickey–Fuller (ADF) statistic, used in the test, is a negative number. The more negative it is, the stronger the rejection of the hypothesis that there is a unit root at some level of confidence.[1]
Contents |
Testing Procedure
The testing procedure for the ADF test is the same as for the Dickey–Fuller test but it is applied to the model
where  is a constant,
is a constant,  the coefficient on a time trend and
the coefficient on a time trend and  the lag order of the autoregressive process. Imposing the constraints
the lag order of the autoregressive process. Imposing the constraints 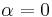 and
and 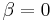 corresponds to modelling a random walk and using the constraint
corresponds to modelling a random walk and using the constraint 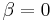 corresponds to modelling a random walk with a drift. Consequently, there are three main versions of the test, analogous to the ones discussed on the Wikipedia page for the Dickey-Fuller test. See that page for a discussion on dealing with uncertainty about including the intercept and deterministic time trend terms in the test equation.
corresponds to modelling a random walk with a drift. Consequently, there are three main versions of the test, analogous to the ones discussed on the Wikipedia page for the Dickey-Fuller test. See that page for a discussion on dealing with uncertainty about including the intercept and deterministic time trend terms in the test equation.
By including lags of the order p the ADF formulation allows for higher-order autoregressive processes. This means that the lag length p has to be determined when applying the test. One possible approach is to test down from high orders and examine the t-values on coefficients. An alternative approach is to examine information criteria such as the Akaike information criterion, Bayesian information criterion or the Hannan-Quinn information criterion.
The unit root test is then carried out under the null hypothesis 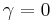 against the alternative hypothesis of
against the alternative hypothesis of 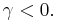 Once a value for the test statistic
Once a value for the test statistic
is computed it can be compared to the relevant critical value for the Dickey–Fuller Test. If the test statistic is less (this test is non symmetrical so we do not consider an absolute value) than (a larger negative) the critical value, then the null hypothesis of 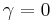 is rejected and no unit root is present.
is rejected and no unit root is present.
Intuition
The intuition behind the test is that if the series is integrated then the lagged level of the series (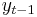 ) will provide no relevant information in predicting the change in
) will provide no relevant information in predicting the change in 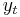 besides the one obtained in the lagged changes (
besides the one obtained in the lagged changes (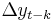 ). In that case the
). In that case the 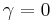 null hypothesis is not rejected.
null hypothesis is not rejected.
Examples
A model that includes a constant and a time trend is estimated using sample of 50 observations and yields the 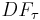 statistic of −4.57. This is more negative than the tabulated critical value of −3.50, so at the 95 per cent level the null hypothesis of a unit root will be rejected.
statistic of −4.57. This is more negative than the tabulated critical value of −3.50, so at the 95 per cent level the null hypothesis of a unit root will be rejected.
Alternatives
There are alternative unit root tests such as the Phillips–Perron test or the ADF-GLS procedure developed by Elliot, Rothenberg and Stock (1996).
Implementations in statistics packages
- In R, the tseries package includes an adf.test function.[2].
- Gretl includes the Augmented Dickey–Fuller test.[3]
- In Matlab, the adftest function [4] is part of the Econometrics Toolbox [5], and a free version is available as part of the 'Spatial Econometrics' toolbox, available at http://www.spatial-econometrics.com/
- In SAS, "PROC ARIMA" can perform ADF tests[6].
- In Stata, the "dfuller" command is used for ADF tests.
- In Eviews, the "Augmented Dickey-Fuller" is available under "Unit Root Test."
See also
- Elliot–Rothenberg–Stock test
- Kwiatkowski–Phillips–Schmidt–Shin test
References
- Elliott, G., Rothenberg, T. J. & J. H. Stock (1996) "Efficient Tests for an Autoregressive Unit Root", Econometrica, Vol. 64, No. 4., pp. 813–836. Stable URL
- Greene, W. H. (2002) Econometric Analysis, Fifth Edition, Prentice Hall: New Jersey. ISBN 0130661899
- Said E. and David A. Dickey (1984), "Testing for Unit Roots in Autoregressive Moving Average Models of Unknown Order", Biometrika, 71, 599–607.